耿合众:用最笨的方法去做
前段时间老是做梦,而且老是梦到自己将要参加高考,关键是老是梦到自己考试时看啥啥不会,做啥啥不懂,提笔忘字,进考场脑子一片空白,洁白的白,常常急出一身冷汗,然后惊醒了。
醒了之后,就很难睡着,夏虫不会为我沉默,尤其是蚊子,在暗夜中不时地进行袭扰,在你看不见的地方给你一个亲吻,留下一个个红包。
睡不着有时候就在想,高考最重要的是什么?是技巧,还是策略,是经验,还是教训。想来想去,觉得许多时候,知识来不得半点虚假,要用笨功夫,做真学问。
说到笨方法,其实也不笨,就像平常去买“笨鸡蛋”一样,其营养价值还是比较高的,不过不要买到假冒伪劣的“笨鸡蛋”。
笨方法,有时候是最接近真相的,是明白清晰的,是简便易行的。
所以今天继续聊高考,主要还是来聊数学试题,看看数学考试中笨方法的使用。
先看题。
甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两个人,另一个人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一个人被淘汰;当一个人被淘汰后,剩余的两个人继续比赛,直至其中一个人被淘汰,另一个人最终获胜,比赛结束。
经抽签,甲、乙两人首先比赛,丙轮空。设每场比赛双方获胜的概率都为1/2。
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率。
看完试题,是不是觉得概率统计的内容,比如回归分析、假设检验,以及二项分布、超几何分布,还有期望、方差等等,真他妈的白学了。
这就是高考试题,永远让你猜不着,猜本身就是一种冒险。
拿到试题,脑海里是不是有三个人轮番挥舞着羽毛球拍比赛,羽毛球在空中飞来飞去,像一只美丽的大蝴蝶,你的心中是不是有一万个草泥马在奔腾,真后悔平时打羽毛球时,没有去用心地排练一下。
羽毛球在飞,可是概率还要去求,第一问容易是送分题。甲连胜四场,实力强悍,所向披靡,独立事件重复发生,4个1/2相乘就行了。
后两问呢,烧脑吧,不妨看看如下解法,先感受一下。


可以吧,有没有一种腾云驾雾的感觉,似懂非懂,终究还是不懂。考场上你能顺利地把第(2)问,第(3)问像上面那样轻松地搞定吗?
说老实话,我第一眼看完这道题,除了第(1)问很快弄出来,后两问还真没有很快地搞定,还差一点就挂了。随着年龄的增长,思维真的不行了,长江后浪推前浪,前浪注定被拍死在沙滩上。
但是,关键地时候有个转折。峰回路转,柳暗花明,你有好技巧,我有笨方法。我们不是聪明人,聪明人大都升官发财去了,天资愚钝的人就要有笨方法。往往最笨的方法是解决数学问题的杀手锏,我把这称为现场模拟,就是把三个人打羽毛球的情景再现出来,通俗一点说就是把实际问题数学化。这时候,我突然想起三句话:用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界。
数学的眼光就是抽象,数学的思维就是推理,数学的语言就是模型。这个过程就是解决问题的过程。于是我这样把这次的羽毛球比赛做了如下的处理:
为了方便,把甲、乙、丙三人分别记为a、b、c,每一次比赛结果胜者在前,负者在后,放在小括号里,比如第一次比赛,甲胜乙负记为a(b),乙胜甲负记为b(a),以此类推。
下面通过这种方法枚举,得出比赛结束时所有可能的结果:

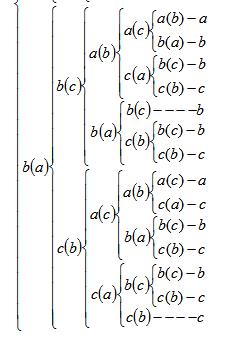
上面最后横线所指的是最终哪一个获胜,根据所列出的结果,一个一个数就行了,这个应该不是难事。

回头看一看,我的笨方法是不是还不错,直观易懂好理解。
但如果把笨方法稍微改进一下,动一下脑子,就可以提高效率。想一想第一局比赛,甲胜乙负与甲负乙胜,是不是很对等,如果列出甲胜乙负的情况,直接把甲乙互换,是不是就是乙胜甲负的结果呢,当然在这个过程中,丙不会受到任何影响,于是清点的时候,数好第一局甲胜乙负所有的结果,自然第一局乙负甲胜的所有结果也就出来了。
这种方法就是初中生,甚至小学毕业生也能够做得出来,这才是数学核心素养,与你高考前拼命刷无数道模拟题无关,与你的老师这样那样押题归纳总结无关。记住,数学是清楚的,数学是明明白白的。
再说一次,下笨功夫,做真学问。用笨方法,也能解决真问题。还记得那年安徽高考数学的概率题吗,好像被称为“品酒师”问题,那个也曾经烧脑的试题,如果把24种结果全部列举出来,所有的问题迎刃而解,那里用的也是笨方法。
实际上,今年的许多数学试题,都能用笨方法很快地解决,只要基本功扎实,不过分地追求技巧,脚踏实地地做个“不聪明的人”,把数学当做数学去学习,而不是为了单纯地应试,那么,一切都就解决了。
有道无术,术尚可求也,有术无道,止于术。就是这个道理。
终南也不一定有捷径,千里之行,始于足下,虚的少一点,实的多一点,你就快乐了。
本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用,绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系(底部邮箱),我们将及时更正、删除,谢谢

