基本不等式详解
基本不等式在高考求最值或范围问题中发挥着重要作用，也具有相当强的技巧性。
从古至今，"比较"都是人类生活中必不可少的部分。有了比较，就有了像 "多、少、一样"等用于描述物体间数量关系的词语，这些词语抽象到数学中，就是我们从小学就熟知的"大于、小于、相等"(其中"大于和小于"我们称之为不等关系)。
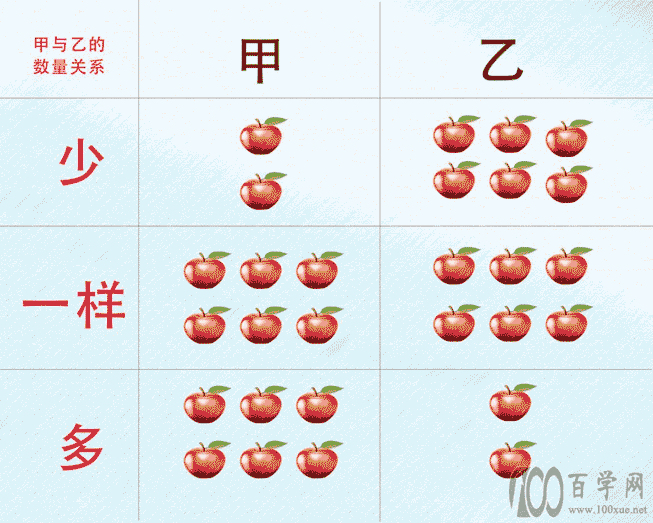
不等关系与不等式
“比较”如果总停留在"多与少"，那生活就永远是一个模糊的概念。但人类文明是在不断进步的，从定性到定量是必然。首先是一、二等数字的引入，然后是数的概念形成，数学中的不等关系变得更清晰了，人们可以借助数来表达物体间的数量关系。如上图中，苹果个数的大小关系的本质蕴含在不等式中：2<6(少),6=6(相等),6>2(多).这是单一的、独立存在的不等关系。
17世纪，伽利略引入函数的概念以后，数学家们使用函数来描述两个变量间的关系y=f(x),函数所体现的是"等量关系"。另一方面，为了处理函数值域的上下界等问题，也有数学家开始使用表达式来描述常量、变量内部及变量间的一类"不等关系"，这样的表达式通常用符号">"或"<"连结(如|x|>0)，现在我们称之为不等式。
早期的"不等式"
由于早期的数学并没有函数的概念、也没有形成">"或"<"等符号，因此当时的不等式都是以文字来表述、使用"不足""超过"等词语体现的，也有部分不等式是后人根据早期数学家发现的等量关系去掉某些部分得到的。
(一).圆周率π的近似值
阿基米德(Archimedes，前287—前212年)使用"穷竭法"计算圆周率π的近似值是早期不等式运用的典型。阿基米德从圆的内接和外接正六边形出发，逐步对边数加倍，直到内接正96边形和外接正96边形为止。阿基米德求出圆周率的下界和上界分别为223/71和22/7，并取它们的平均值3.141851为圆周率的近似值。
从方法上，"逼近思想"在一定程度上就是不等式思维的体现，从结果上看，π的近似值
223/71<π<22/7 本身就是一个不等式(尽管阿基米德没有用真正的不等式表示)。因此，是否可以这么说——阿基米德是第一个清晰使用并记录不等式的人。
(二).无理平方根的近似计算
另一个运用不等式求近似值的例子是开平方。早在公元1世纪，古希腊著名数学家就运用"平方根倍位法"来求无理平方根的近似解。在运用海伦公式
求三角形面积时，经常会遇到类似求√720的解，海伦采用了下面的方法：
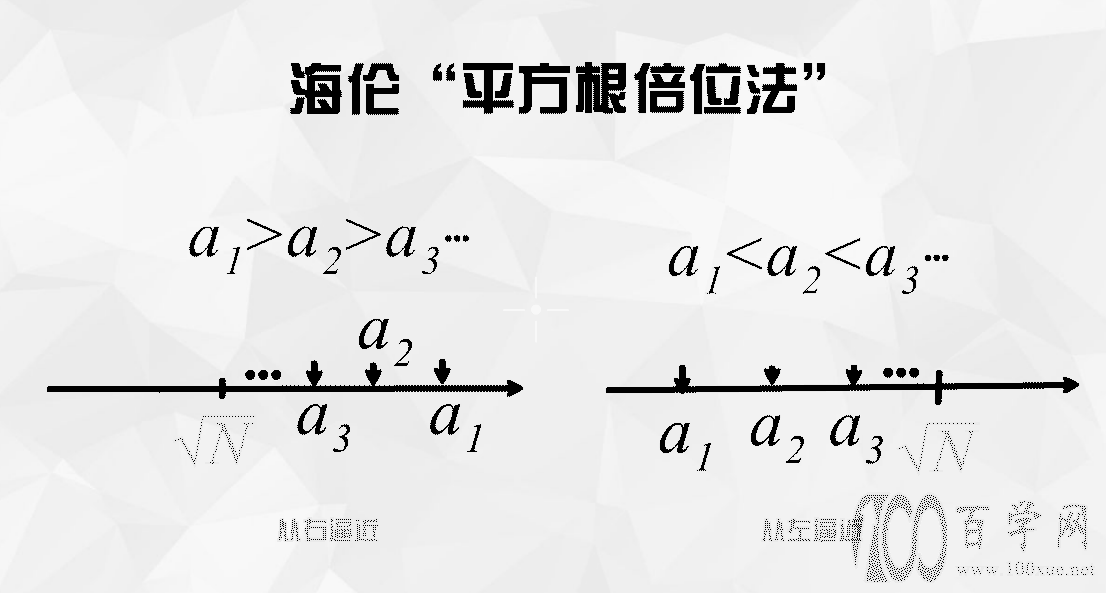
另外，这一类公式
在我国古代(名曰："不加借算")、古印度及古阿拉伯等国家很早都被广泛使用.其原理，都是运用不等式找上界或下界，通过重复的不等式运算(迭代)得到平方根的近似值。
(三)三角不等式
毕达哥拉斯以后的古希腊数学，主要以几何为数学的基础。因此，下一个早期出现的不等式是几何的，而且我们再熟悉不过，它以文字的形式出现在欧几里得(Euclid，约前330年-前 275年)的数学巨著《几何原本》(第一卷命题20)中——"三角形的两边之和大于第三边"。用不等式符号表述为："在边长分别a,b,c三角形中，恒有a+b>c.".
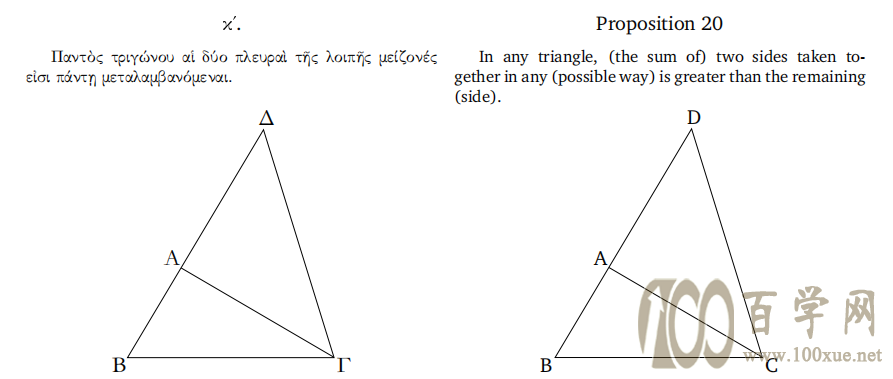
这是一个显而易见的结论，在几何学中的重要性也毋庸置疑。在解析几何被发现以后，三角形不等式更是被赋予了向量表示和坐标表示。
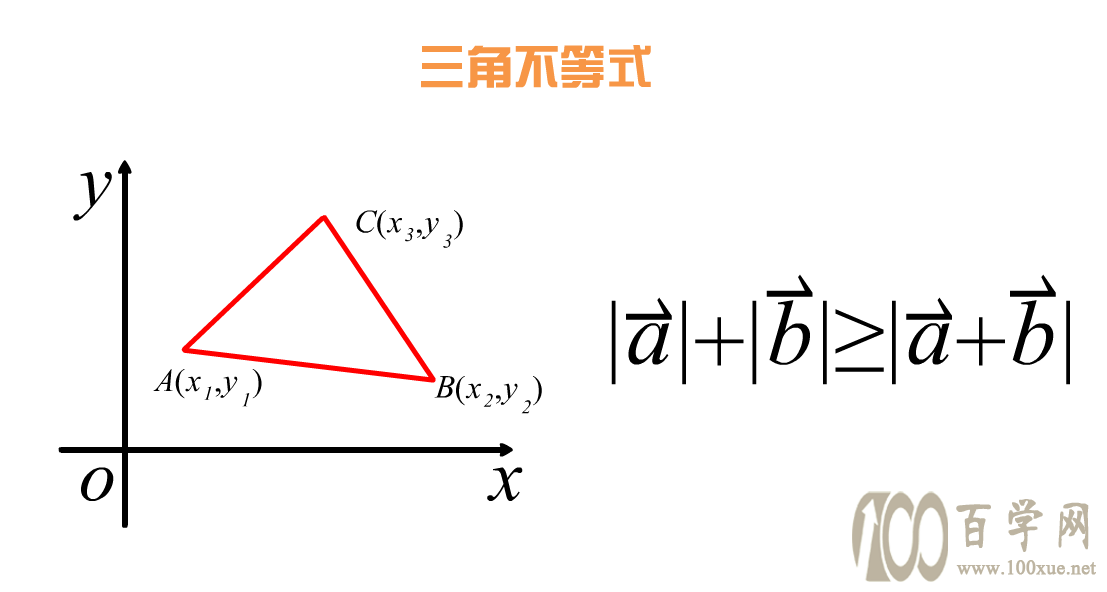
(四)基本不等式的两个等价形式
《几何原本》还赋予了另一个重要的不等式以几何意义，当然，也许这并不是欧几里得本人的意愿，但是后人还是把第一次阐述并证明二维基本不等式(AM-GM)的功劳归功于他。
，
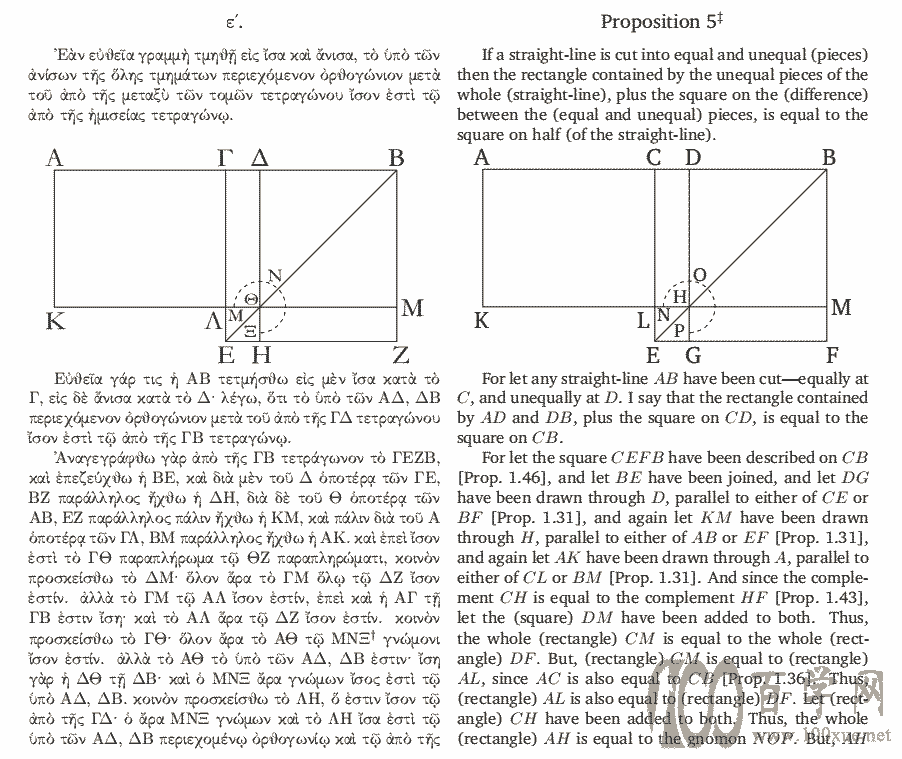
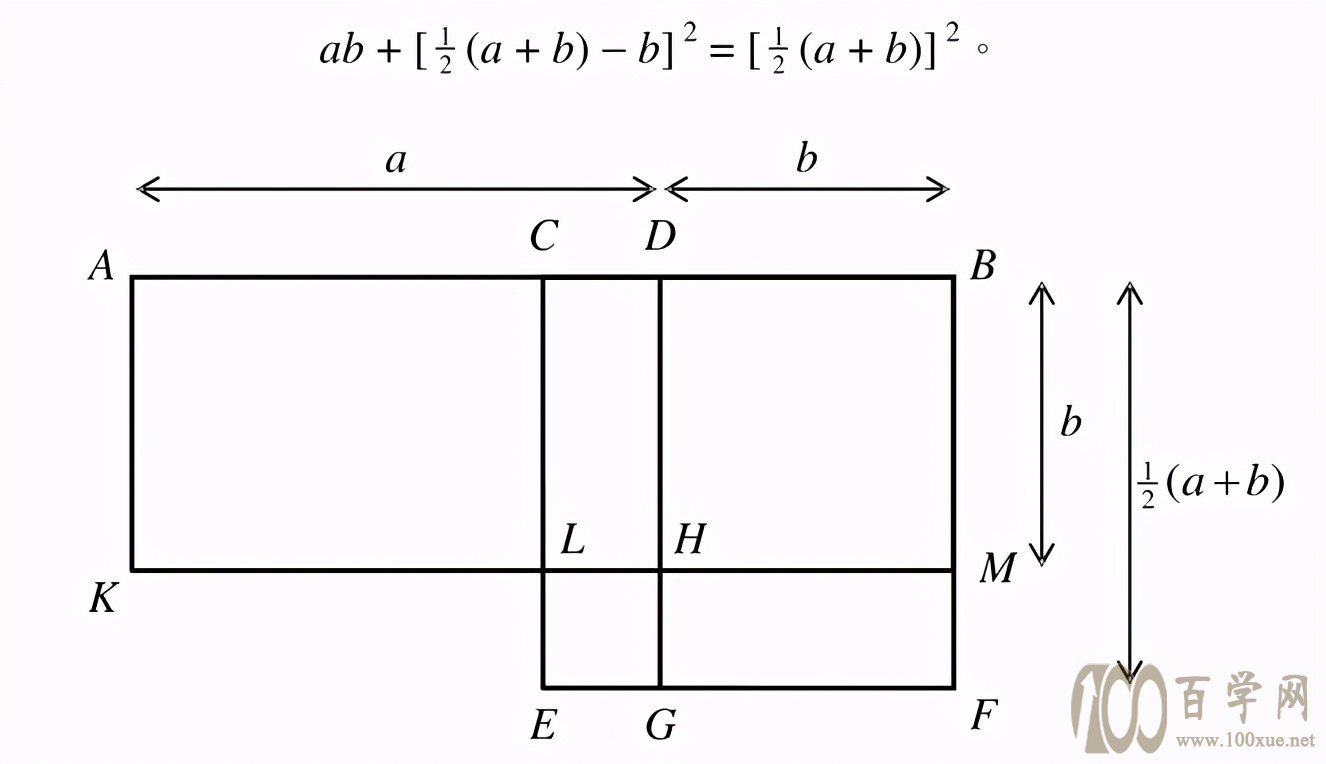
从《几何原本》第二卷命题五可以看出，欧几里得阐述并证明了以下等式：
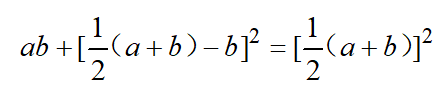
如果我们将正方形LEGH的面积略去，便得到二维形式的AM-GM不等式：
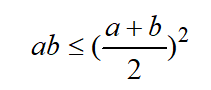
与欧几里得《几何原本》中的记载有异曲同工之妙，我国古代三国时期著名数学家赵爽在给《周髀算经》作注时，创制了一幅"勾股圆方图"(赵爽弦图)，用形数结合得到方法，给出了勾股定理的详细证明。
如图，以弦为边的正方形的面积等于四个直角三角形(朱实)的面积加上以股减去勾为边的正方形(黄实)的面积。即，
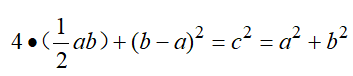
如果我们去掉"黄实"部分面积，也可得到基本不等式的变形——重要不等式：
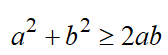
当然这里的a和b都是正数(边长不能为负数)。
尽管基本不等式被"发现"的时间较早，但是在很长一段时间内它并未引起数学家们的注意和重视，下一个重要突破由麦克劳林(Maclaurin，1698-1746)给出。麦克劳林在1729年，根据插值和对称不等式相关知识，构造了以下的著名不等式——麦克劳林不等式：
这个不等式链的神奇之处在于，它包含了基本不等式，而且AM不等式在其最左边，GM不等式在其最后右边.下面是当n=4时候的麦克劳林不等式.
麦克劳林不等式基于对称不等式，无论之于式子的对称性、和谐性、简洁性，还是不等式的实用性，都具有较高的数学欣赏性和自然美感。但是也有遗憾，基本不等式有一个拓展的不等式链——均值不等式， 麦克劳林不等式并不能包含平方平均数和调和平均数。
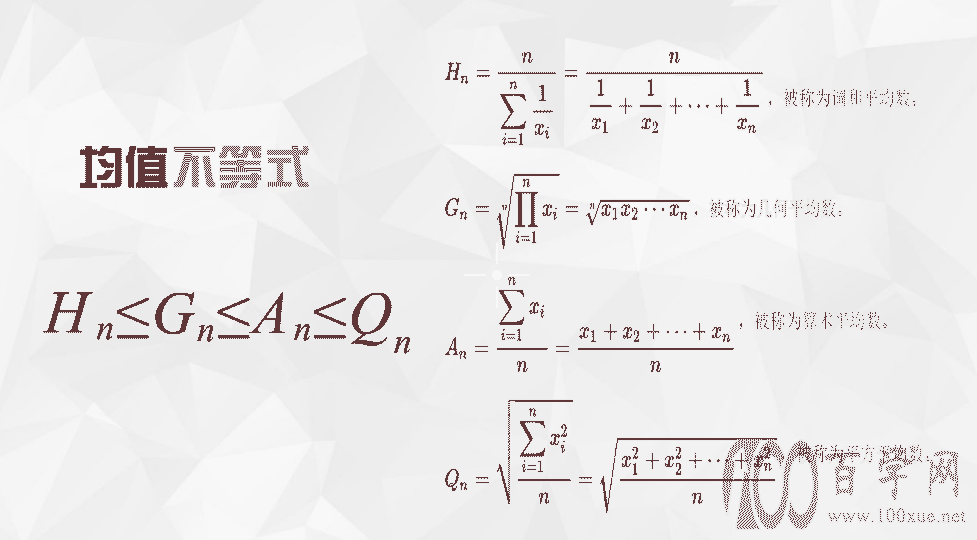
于是，再过了一个多世纪，德国数学家赫尔德(Hölder,1859-1937)通过"赫尔德均值"定义下的"广义均值不等式"弥补了这一遗憾。
(五)伯努利不等式
另一个早期不等式是"伯努利不等式"，它由雅各布(Jacob Bernoulli，1655-1705)在
1689年的文章"Positiones Arithmeticae de Seriebus Infinitis"中首次发表，并多次使用该不等式进行证明。
"伯努利不等式"在高中数学中仍然占有较高的地位，人们对伯努利家族的崇拜、以及历史的演变使得对这个不等式的发现深信不疑。但是它也可能被张冠李戴了，根据1963年Hofmann的最新研究，"伯努利不等式"的发明权应该归属于斯鲁兹(Sluze,1622-1685),因为在Mesolabum(1668)中，他引入了不等式链：
如果我们将各项叠乘，可以轻松得到伯努利不等式。当然，这样的发现是间接的，而伯努利的不同之处在于直接给出了不等式。
(六)柯西不等式
柯西不等式，严格意义上说，应该叫做【柯西-布尼亚科夫斯基-施瓦茨(
Cauchy-Bunyakovskii-Schwarz)不等式】，名字听起来既长又奇怪.他首先由法国数学家柯西在Cours d'analyse de l´Ecole Royal Polytechnique(1821)中以注释的形式给出柯西不等式(离散)的简单形式，及特殊情况的证明。
接着，柯西的学生布尼亚科夫斯基在1859年的论文中，给出了柯西不等式的积分形式。
施瓦茨(Schwarz ，1843-1921)在d ¨Uber ein die fl¨achen kleinsten fl¨acheninhalts betreffendes problem der variationsrechnung(1888年)中，给出了柯西不等式积分形式的严格证明.
不等式的符号表示
我们都知道，在17世纪，有2个重要的不等号的符号表示，即英国数学家奥特雷德(Oughtred，1574-1660)的 
，
，以及英国哈里奥特(Harriot，1560–1621)的"<"或">"。但在接下来的1个多世纪，由于Oughtred的Clavis Mathematicae比Harriot的代数作品更受欢迎，因此，明显人们更多地使用Oughtred的不等符号。
但为什么今天我们最终选择了"<"和">"呢?可能有这样的一些原因：一、Oughtred在自己的部分作品用也使用了这个不等符号，要知道，Oughtred的作品广受欢迎，而他自己并没有坚定的使用自己的符号，是否也觉得自己的符号写起来不方便呢?二、19-20世纪包括Cajori (1859-1930) 在内的数学家发文关注到了，Oughtred不等符号书写的困难，这对Oughtred的符号使用时具有负面引导性的。当然，笔者觉得，如果把这两类符号给小学生选择，他们依然会选择"<"和">"，数学应该尽可能的书写简洁。
接下来的一个重要符号由18世纪数学家给出， 1734年,法国测量员布格(Bouguer，1698 - 1758)给出了符号"≤" 和" ≥"，并沿用至今。
作为数学概念的不等式
前文介绍了许多重要的不等式，它们分布在几千年的数学文明之中，纵然17世纪就已经有了不等式的符号表示，数学们也尝试用数学家的名字来命名不等式，但直到20世纪，不等式知识都是零散的、不严谨的。数学家们只是把它作为一个解决问题时需要的工具，在极限等模块中大量使用，即使像柯西这样的数学大咖，也没有从一个系统性的角度来研究不等式。
直到1934年，第一本研究不等式的书籍——哈代-李兹伍德-波利亚合著的《不等式(Inequalities)》问世，才让不等式正式走向数学舞台的台前。同时，哈代(Hardy，1877-1947)还作为the Journal of the London Mathematical Society杂志的创始人，这个杂志为不等式的相关论文发表提供了便利。为此，哈代被誉为"the father of the Discipline of Inequalities".
《不等式(Inequalities)》的发表，似开了闸的水库，让不等式这个被禁锢了千年的数学之子喷涌而出，自此一发而不可收拾。不等式从数学中脱颖而出，第一次作为独立的数学概念(甚至学科)而存在，直至今日，都在数学中扮演了重要角色，也成为各类数学竞赛的"宠儿"。
基本不等式高考真题(1999~2021)汇总，含讲义和答案
本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢