2022CMO第二题与猫爪定理——暨猫爪定理之十二

　　2022年第38届中国数学奥林匹克(简称CMO)于12月29日30日举行，每天早上8：00-12：30考试，解答三个题目。由于疫情，今年的CMO全部采用分省线上举行，每个省设立一个考场，同步考试。

　　第一天的第二题为几何题，本文记录一下本人对此题的思考解答过程。

　　题目为：

　　初看题目有点复杂，只能先画一个草图分析一下。

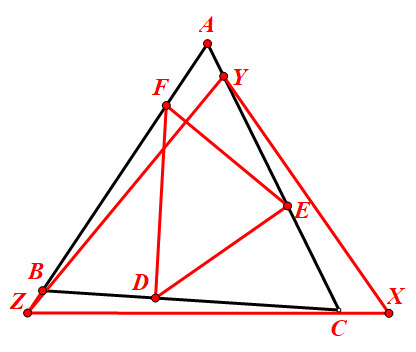
　　草图大概如上，已知中的关键是

　　DE/20=EF/22=FD/38,说白了就是△DEF的三边之比为20:22:38即10:11:19,

　　取20，22，38意义明显，因为是2022年第38届CMO。这三个数字应该没有什么具体的意义，可以理解为△DEF三边比值为定值，即其形状是固定的。

　　涉及到三角形的内接三角形形状固定的问题，容易想到一个著名的定理——猫爪定理(即密克定理，因为其形状类似猫爪，本人戏称之为猫爪定理)!形状固定则说明DEF对△ABC的密克点P为定点，这很容易倒角证明。利用正弦定理知道PA:PB:PC=11:19:10。

　　下面考察△XYZ,类似的由DE⊥XY，FE⊥ZY，DF⊥XZ，可知△XYZ形状与△DEF相同，即相似，

　　从而其对△ABC的密克点也是P点。

　　这样，我们就可以尝试画出准确的图了，先在单位正△ABC内部取点P，使得

　　PA:PB:PC=11:19:10，这样的点P是唯一确定的。在BC线段上任取一点D，圆DPC交AC于E，

　　圆EPA交AB于F，圆FPB又会交AC于D。即动点D确定了△DEF，

　　由DE⊥XY，FE⊥ZY，DF⊥XZ，

　　知△XYZ应该也就由D确定了。

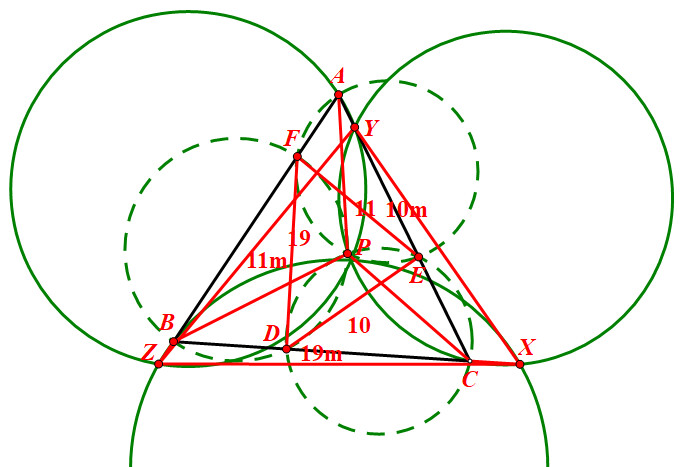
　　到底是如何确定的呢?由垂直及共密克点P可得△PDE∼△PXY，由DE⊥XY得DP⊥XP。这就能由D和P确定X，只需过P作DP垂线与BC交点即为X。

　　这样就能准确得作出图形，似乎性质也挖掘得差不多了。

　　下面考虑从结果入手，题目要求出两个三角形面积得倒数和，可能是一个定值，也有可能是某个范围。△DEF和△XYZ在变化，需要找一个参数或者不变量来表示他们，这很容易想到，因为P对△ABC的密克三角形都是相似的，这里面是有一个最小的三角形，即P的垂足三角形LMK，D运动，不妨引入一个角度，设

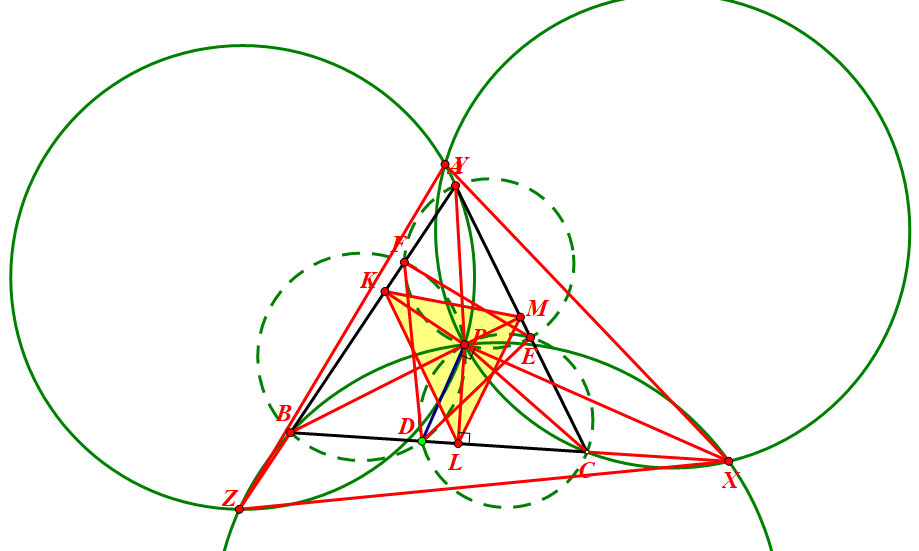
　　设∠PDL=θ,则∠XPL=θ,

　　故PDsinθ=PL=PXcosθ,

　　设△LMK面积为S',由相似得

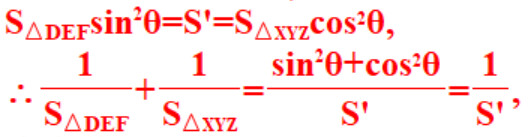
　　为定值!这样这个题目得思路基本就差不多了。

　　下面乘胜追击，考虑如何求出△LMK面积S'。

　　可以设PA=11x,PB=19x,PC=10x,下面需要把x求出来，即要得到一个含有x得等式。本质上就是得到一个含有PA,PB,PC,AB,BC,CA的一个恒等式。最自然的思路是用勾股定理或者余弦定理以及和角公式，这是一般性的思路，自然但是比较麻烦。考虑到正三角形的特征，要得到这个恒等式，常见的思路是将PA,PB,PC依次旋转出去得到三个正三角形，另外三个三角形全等且边长恰好是PA,PB,PC。对此六边形面积算两次即得，具体过程为：

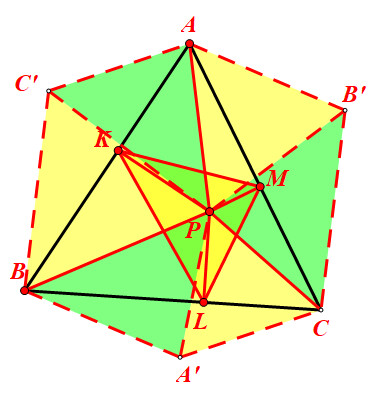
　　这就是最终结果了。

　　这就是本题的大体思路，不过里面还要考虑到图形的特征及形内形外等，需要再缜密叙述和考虑一些特殊情况。最后将结果整理出来，书写如下：

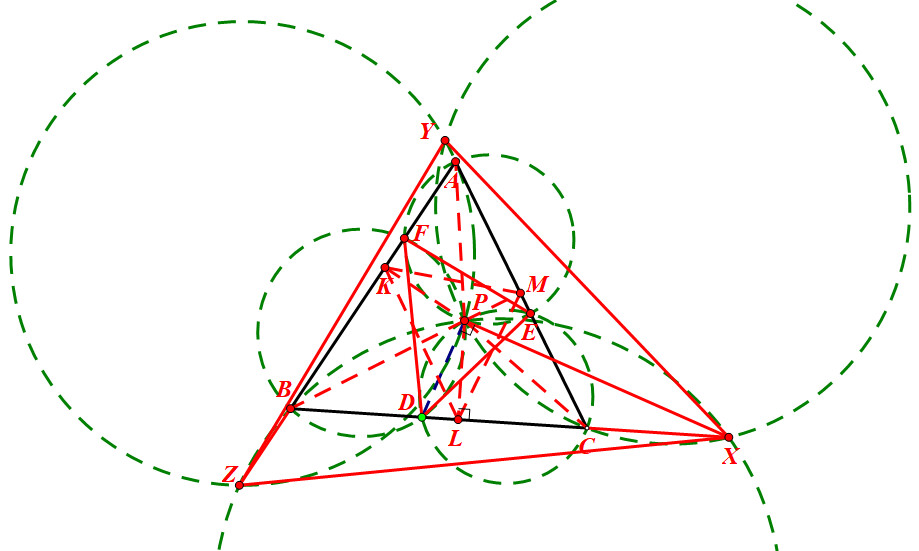
　　证明：

　　设圆CDE和圆AFE交于点E,P,

　　则∠AFP=∠CEP=∠BDP,

　　故BDPF共圆，

　　即圆CDE，圆AFE，圆BDF共点于P。

　　由正弦定理得PA=EFsin∠AFP/sin60°,

　　PB=FDsin∠BDP/sin60°,

　　PC=DEsin∠CEP/sin60°,

　　故PA:PB:PC=EF:FD:DE=22:38:20=11:19:10,

　　∠BPC=∠BAC+∠ABP+∠ACP

　　=∠BAC+∠FDP+∠EDP=∠BAC+∠FDE,

　　同理∠APB,∠CPA也为定值。

　　由于D,E,F在线段BC,CA,AB上，

　　故P点在△ABC内部，且是唯一的一点。

　　由DE⊥XY，FE⊥ZY，得∠XYZ=∠DEF,

　　同理∠YZX=∠EFD,

　　故△DEF∼△XYZ,

　　同理可得圆CXY，圆AZY，圆BXZ共点于P。

　　∴△PDE∼△PXY,

　　∴PD⊥PX.

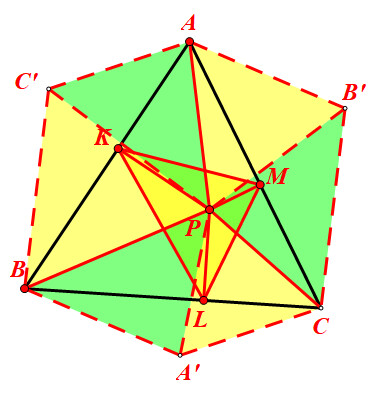
　　最后做一个简答的总结与评价：

　　本题结构初看比较复杂，但是只要能想到经典的猫爪定理(即密克结构)即可获得入手点，想到△DEF密克点为定点，进而发现△XYZ密克点也为点P，再得到PD⊥PX即可获得极大进展。下面由简单的三角计算得到所求结果为定值。最后登堂入手，通过代数计算出定值即可。

　　通过上述过程看来本题“似乎”不难，不过具体解决的时候可以发现很容易误入歧途，有不少地方还是不宜突破的。例如本题入手点相对单一，必须熟练密克结构。有的同学对密克结构不够熟悉，要么想不到密克点，要么想不到P点为定点。本题最困难的地方是最后垂足三角形KLM面积的计算，理论上就是得到一个含有x的等式，是一定能算出来的，方法也挺多的，可以用三角函数和差角公式、余弦定理，甚至还可以用向量、复数或者解析法，当然也可以用上述相对偏几何的方法(本质上是费马点问题)，不同的算法结果虽然殊途同归，但是计算量的差距还是蛮大的，有的计算会比较复杂，数字很大。还有计算出x以后，算△KLM面积的时候如果不用海伦公式，用大三角形面积减去三个小三角形面积，也会陷入复杂的计算之中。当然还有一个很重要的问题是，题目中没有给出图形，上述的解法是非常依赖图形的相对位置的，所以严格上讲还要考虑图形的位置，以及点P与△ABC的位置关系等。所以上述偏几何的解答未必完整，书写也未必规范，特别是在倒角的过程中，不同图形角度关系是有一定区别的，所以在解答中也容易由于考虑情形不全面而被扣分。

　　当然本题的本质就是四个点构成的六条线段长度之间存在一个恒等式，一般的情况下会是一个六次齐次式，对于本题结果会得到一个含有x^2的双二次方程，理论上是可以通过一元二次方程求根公式得到的。而且上述密克结构对任意△ABC都成立，因此本题也可以考虑将结果推广到一般的给定的任意△ABC中，不过计算量会大不少，结果也会不那么美观。

　　综上而言，本题还是一个不错的题目，一言以蔽之，就是上手容易满分难。本题入手相对容易，毕竟几乎所有参赛学生都了解密克结构，就是通过共圆、倒角、相似处理问题。得到一些简单的几何性质以后就能通过基本的计算得到所求结果为定值，这应该都是得分点。当然要算出最后的定值还是很有难度的，据听说完全解答出本题的学生并不多。所以本题的区分度应该很好，通过思考和计算的深度可以把不同水平的学生有效的区分出来。

　　猫爪定理(即密克结构)应该是很火的话题，本公众号也写过一系列相关文章。前两天江泽民主席去世的时候大家为了纪念他，又大量发布了“江泽民定理”，本质就是猫爪定理(即密克定理)。本系列的第一篇文章就介绍过此定理。感兴趣的读者可以自行参考。本题及本文也算是对江泽民主席的另一种缅怀。

　　作者：金磊几何

本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢