两圆一线解决等腰三角形存在性问题
一、两圆一线模型
条件:平面上两定点A、B。
要求:找一动点C,使△ABC为等腰三角形。
解析:要使△ABC为等腰三角形,那么有以下三种情况:
①AB=AC
②AB=BC
③AC=BC
第①种情况AB=AC,AB和AC有交点A(定点),要AB=AC就是平面上有两点,这两点到A(定点)的距离相等,距离为AB(定长),可以利用圆上每一点到圆心的距离相等来找点C.(下图C1)
第②种情况AB=BC,AB和BC有交点B(定点),要AB=BC就是平面上有两点,这两点到B(定点)的距离相等,距离为AB(定长),可以利用圆上每一点到圆心的距离相等来找点C.(下图C2)
第③种情况AC=BC,AC和BC有交点C(动点),要AC=BC就是平面上一动点到两定点的距离相等,可以利用垂直平分线的性质(垂直平分线上的点到线段两端点的距离相等)。
(下图直线L)

二、解题方法
等腰三角形存在性问题一直是中考的“宠儿”,也是考生们的“梦魇”。今天就来看下等腰三角形存在性问题的考法和做题技巧。
考法:
①、求满足情况的动点的个数(选择题)
②、求满足情况的动点的坐标(26题第二问)
做题步骤:
①、找两定点并连接两定点
②、作两圆一线模型
③、找两圆一线与动点运动轨迹的交点
④、利用两点距离公式求交点坐标(可以去掉根号,注意考虑两个解是否都满足情况)
三、题型分类

解析:这道题的考点为等腰三角形的存在性问题。第一步:找定点定线段,;第二步:作两圆一线模型;第三:找两圆一线与动点轨迹的交点。
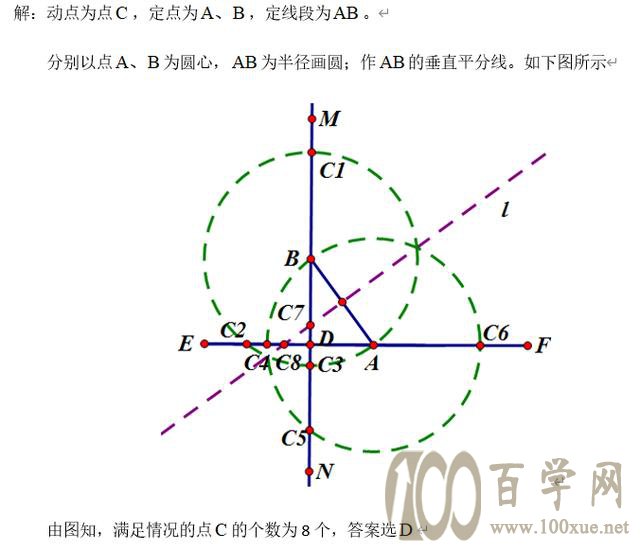

解析:这道题的考点为等腰三角形的存在性问题并且需要求动点坐标。第一步:找定点定线段,;第二步:作两圆一线模型;第三:找两圆一线与动点轨迹的交点;第四:利用两点间距离公式求交点坐标(注意数形结合不要遗漏解)



本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用,绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系(底部邮箱),我们将及时更正、删除,谢谢

