2020年中国女子奥林匹克第一题的证明

　　2020年中国女子数学奥林匹克(简称CGMO)于8.8日至8.12日在江西鹰潭一中举行，来自全国各地的33支代表队共133名学生参加比赛。个人总分前12名自动进入数学冬令营。今年因为疫情影响，国外的选手无法直接参加，部分国家通过网络参加。

　　考试时间为8.9日下午14：30-18：30和8.10日上午8:00-12:00.每天四个题目，其中几何题为第1题和第7题。

　　本文写一下本人对1题的思考过程。

　　第一题为：

　　已知：四边形ABCD中，

　　AB=AD,CB=CD,∠ABC=∠ADC=90°,

　　E,F在线段AB,AC上，P,Q在线段EF上且AE/EP=AF/FQ,

　　BX⊥CP于X,DY⊥CQ于Y。

　　求证：P,Q,Y,X共圆。

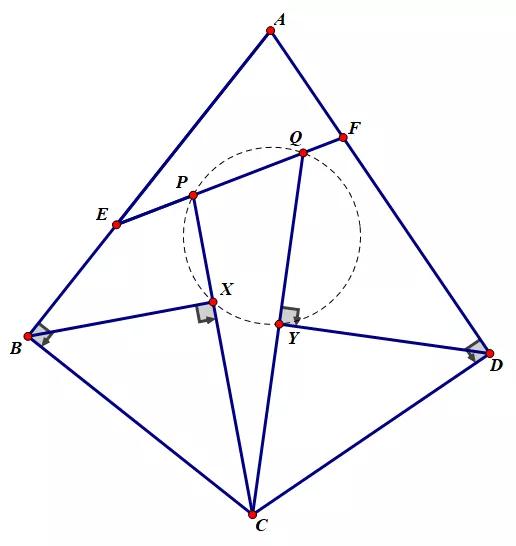
　　思路分析：

　　先画出准确图形，已知条件中除了对称及比例式外似乎没有什么好的性质。

　　从结果入手看看，

　　要证明PXYQ共圆。首选倒角或者倒比例，

　　根据图像，最自然的思路是证明CP*CX=CQ*CY.

　　等价于证CP/CQ=CY/CX.

　　但是已知条件中的相等、垂直及比例都不好用，

　　计算是最容易想到的，但是也不容易实施。

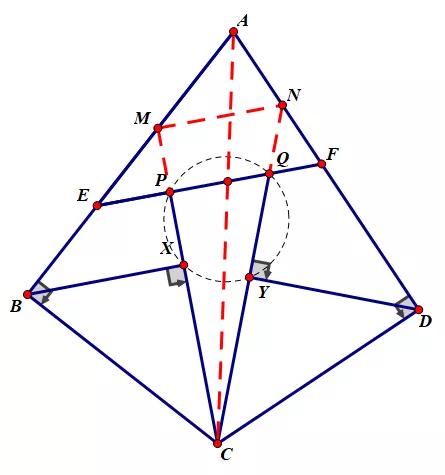
　　通过探索，发现要利用直角及垂直和CB=CD表示CX,CY,

　　一个合理的想法是延长CP,CQ交AB,AD于M,N,

　　则CX*CM=CB^2=CY*CN,

　　则需证CM/CN=CP/CQ,即证MN//EF.

　　这样就能消去X,Y,B,D,得到下图，

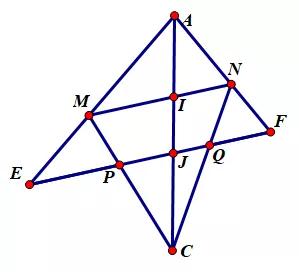
　　简化为：已知∠CAE=∠CAF及AE/EP=AF/FQ,

　　求证MN//EF,

　　容易想到平行很好用，不妨考虑其逆命题，即先由平行证等比例。

　　这个不难用平行线性质(即线束定理)及角平分线定理及等比定理证明。

　　具体证明如下：

　　AE/AF=JE/JF=IM/IN=JP/JQ=(JE-JP)/(JF-JQ)=EP/FQ,

　　下面不难用同一法证明其逆命题，从而命题得证.

　　最后将证明整理如下：

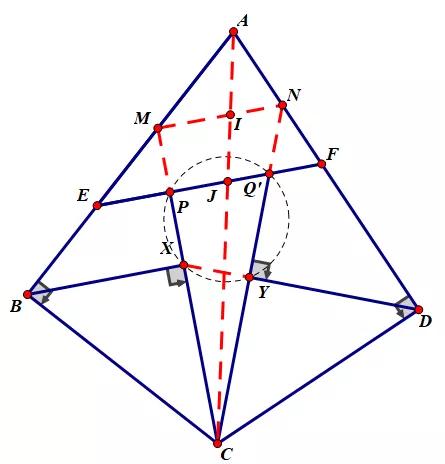
　　证明：

　　设CP交AB于M，作MN//EF,且N在AD上，

　　NC交EF于Q',AC交MN,EF,于I,J.

　　由对称性得∠BAC=∠DAC,则

　　EP/FQ=AE/AF=JE/JF=IM/IN=JP/JQ'=(JE-JP)/(JF-JQ')=EP/FQ',

　　故Q,Q'重合，即NQC共线。

　　则CX*CM=CB^2=CD^2=CY*CN,

　　∴CX/CY=CN/CM=CQ/CP,

　　∴PQYX共圆。

　　无独有偶，昨晚做完这个题目，早上我的邮箱收到了王正良同学寄来的一个他的解答，他也是用平行线性质证明的，没有用到同一法，他是通过作PG//AB，得到QG//AC来完成证明的。我们的证明大同小异、

　　异曲同工，他的证明如下：

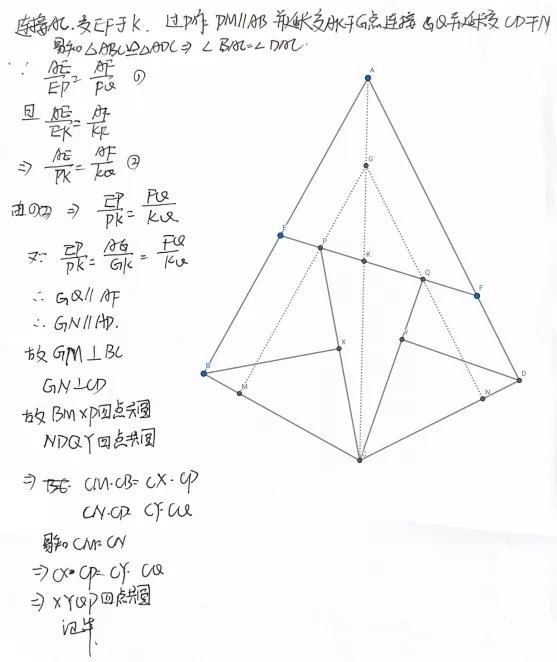
　　本题是一个难得的简洁而有趣的问题，解决他的关键在于如何利用比例这个条件，要么像我那样做出M,N,发现MN//EF。要么如王正良同学那样直接作平行线。当然应该还有其他添辅助线的方法。直接建系或者三角计算当然也是可行的。

本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢