竞赛1：光滑水平块内单摆水平振动周期

　　试题预览

　　光滑的水平地面上有一质量为 M 的滑块，滑块表面有一质量可以忽略的钉子 O ， O 处绕着长为 l 的轻绳，绳下系着质量为 m 的小球，开始时系统处于静止状态，如图1所示，轻绳与竖直方向有一很小的夹角 θ_0 ，然后让小球自由摆下，形成自由振动，设小球摆动过程中不会与滑块表面接触，也不会与地面接触，且滑块不会倾倒，试求小球的摆动周期。

　　解题步骤

　　光滑水平块内单摆水平振动周期

　　方法一：引入惯性力修正后，小球m的受力分析如图2所示，不妨设小球m运动到角度为θ时的加速度为ω

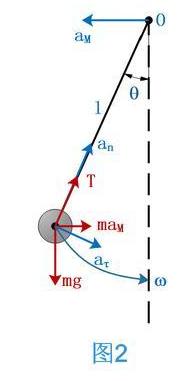
　　则小球m切向受力分析可知：

　　mgsinθ+maMcosθ=maτ (1)

　　小球m法相受力分析可知：

　　T+maMsinθ-mgcosθ=maη (2)

　　对框架M受力分析可知：

　　Tsinθ=MaM (3)

　　考虑角量与线量的关系，可得：

　　aτ=lβ

　　aη=ω2l

　　则，在θ 0时，cosθ 1，sin θ，则(1)(2)(3)(4)，可化简为：

　　lβ=gθ+aM

　　mω2l=T+maMθ-mg

　　aM=Tθ/M

　　故，可解得绳中的拉力为：

　　T=mg+mω2l+m/M Tθ2 (6)

　　忽略角度高阶小量后，可得：

　　T=mg+mω2l (7)

　　将上式代入到方程(1)，化简可得：

　　(1+m/M)gθ+m/M ω2lθ =ld2θ/dt2 (8)

　　考虑到θ 0，则ω 0，即ω2 0，则上式可化简为：

　　(1+m/M)gθ=ld2θ/dt2 (9)

　　故，小球将做简谐运动，即小球的振动角频率为：

　　ω0=√(M+m)g/Ml (10)

　　则，小球振动周期为：

　　T=2π/ω0=√Ml/(m+M)g (11)

　　方法二：

　　考虑质量为m的小球由角度θ0下落到平衡位置的过程，由于没有非保守外力的作用，因此运动过程中系统保持机械能守恒，即：

　　mgl(1-cosθ0)=1/2mv2+1/2Mv2M (12)

　　由于水平方向没有收到外力的作用，因此系统水平方向上动量守恒，即：

　　mvm =MvM (13)

　　并假设平衡位置的角频率为ω0，则平衡位置的速度可表示为：

　　vm=ω0lθ0 (14)

　　故，联立方程(12)(13)(14)，可解得：

　　2gl(1- cosθ0) = (M+m)/M ω02l2θ02 (15)

　　故，当θ0 0时，由cosθ0的泰勒级数展开可得：

　　cosθ0 = 1-1/2θ02 (16)

　　即，上式可化简为：

　　2glθ02 = (M+m)/M ω02l2θ02 (17)

　　故，小球的振动角频率为：

　　ω0 = √(M+m)g/Ml (18)

　　则，小球的振动周期为：

　　T=2π/ω0=√Ml/(m+M)g (19)

　　模拟重现

　　方法分析

　　从上面小编给出的解题思路和方法可以比较明确的看出来，由于该题目非常类似于动力学的一般题目类型，因此同时存在多种解决这类题目的思路和方法，类似于动力学的一般方法，通常从受力分析的角度分析解决题目，或者从能量的角度分析和解决问题，当然了，就这个题目而言，从能量的角度上来分析问题并不比从受力分析的角度上来解决问题有着明显的优势，因此小编并没有给出从能量角度上解决这个题目的思路和方法，当然了，同学们如果有兴趣的话，可以自己尝试一下从能量的角度分析和解决问题，同时这个题目由于单摆运动的滑块并不是静止不动的，因此在运动过程中，滑块必然要发生运动，且并不是匀速直线运动，这一点从模拟重现中就可以看出来，当然了仔细观察模拟重现的情况，同学们也应该能够注意到，这个滑块其实也是做简谐振动的，且振动周期与单摆的周期相同哦，其实这个题目完全可以进一步让同学们计算一下滑块的运动方程。

　　当然了，对于这样的题目类型，从受力分析上解决问题的题目类型，不仅仅可以直接受力分析，也可以引入惯性力修正后，转化为惯性系下解决问题，这样可以稍微简单一点儿，这样的两种思路吴老师都已经给出了。

　　高效学课堂

本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢