2021年国际城市数学锦标赛试题

　　又拖更了好久, 上次发Kürschák József的时候其实赵博士就发的是两个文件给我, 但是上次发了之后懒了一天, 然后公司突然一大堆事情忙到前天. 中间的时候赵博士又给我发了今天这个锦标赛的题, 也是忙到没时间整. 结果昨天赵博士又给我发了Metropolises的题... 感觉我再不翻出来赵博士要打人了...... emm, 反正我还有一大堆调休架, 大不了休息一天好了.

　　于是昨天半夜熬着把锦标赛翻出来了, Metropolises的题可能明天发, 因为昨天赵博士给我发的只有一半, 另一半还没放出来, 那我还是等着完整版再发好了. 反正今天发的这个, 也算是突破我的历史长度了 (吐血)...

　　不过u1s1, 这个比赛其实, 中间混进来了一大堆脑筋急转弯题? 而且还是很俄式的脑筋急转弯, 反正赵博士把俄文的答案也给我了, 那我就挨个提一下答案好了. 但是可以先说一下, 如果还是数学竞赛的初学者的话, 可以做一下O初的P4, P5, O高的P3, P5, A初的P4, P6, P7, 还有A高的P4, P5和P7. 但是如果不是初学者的话感觉好像只有O高的P5, A初的P6, P7和A高的P5, P7可以做做看看. 不过下面还是按顺序给答案好了.

　　O初P1. 小学题, 4次...

　　O初P2. 就, 设一下边长硬解都可以, 答案是2,3,4,24.

　　O初P3. 每个袋子拿一颗出来, 就好了. 这题刚翻出来我都怀疑我翻错了? 就? 这题感觉就应该放在第一题吧? 脑筋都不用转弯都可以做......

　　O初P4. 就, 如果等腰三角形的底边不是对角线的话, 那么边形的这个内角就只能是锐角啊, 然后凸形的内角就只能有三个锐角...... 所以边形的边的话至多就只能分三段, 每段里面每条边长度相等. 那么任意四条边就有两条相等.

　　O初P5. 反证. 如果存在两个人执白赢的局数相同, 那么这两个人就一定有一个人不比另一个人弱, 矛盾. 所以每个人执白赢的局数不同, 只能是, 也就是说有一个人执白赢了所有人. 同理也存在一个人执黑赢了所有人. 如果, 那么这人就不是不比任何人弱了, 这人直接比所有人都强... 所以, 那么这两个人之间的执白执黑的棋局就只能两人都获胜, 矛盾. u1s1这题翻出来之后第一反应觉得是个图论题, 而且要比较两个竞赛图的度数, 不过这答案给出来的做法一点图论的感觉都没有, 还挺神奇的.

　　O高P1. 脑筋急转弯题, 显然好数没有平方因子, 那么被整除的都不是, 所以至多连着三个, 然后显然和都是, 所以三个.

　　O高P3. 答案是, 而且构造还挺好想的. 实际上初始状态时, 甲如果只染一个格子的话, 显然染中间那个是最优的, 染两个格子的话脑补一下就应该想得到, 如果记中间的格子是的话, 那么染的就应该是和, 或者染竖向的对应格子. 然后证明我懒得看了, 毕竟答案是俄文的... 不过这个题如果改成初始是染三个格子的话还挺有趣的, 这难度一下子就彪起来了.

　　O高P4. 就... 垂心只能是满足和构成正三角形的点, 这样的话和的一共四种选择得到的垂心还只有两个, 固定圆这个说法就...... 莫名离谱? 因为虽然我不会几何, 但也想得到对称性, 怎么想这些垂心都在中垂线上, 那共的这个圆不就只能是广义的了吗? 结果好嘛, 设的可能位置为和, 结果是一个垂心组?

　　O高P5. 这个题还挺有趣的. 答案我都没读, 就看到答案里面一图就懂了:

　　A初P1. 只能是和. 满足数列为和.

　　A初P2. 都可以, 答案也是俩图:

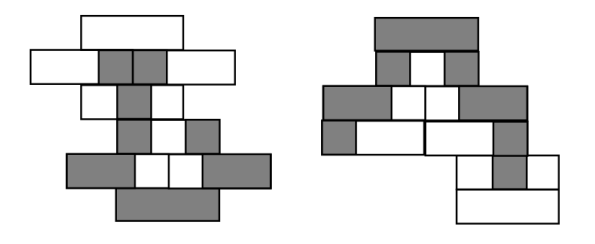
　　A初P3. 可能值只有. 这个一画出图来就懂了, 嗨在挺好做的. 不过这答案还给了四个解法....

　　A初P4. 这题翻出来之后第一感觉是这游戏能赢? 感觉两方都可以恶意搞得对面赢不了才对啊? 结果答案真的是都赢不了... 不过这个答案给的操作有点猥琐, 看了一下意思是每个人的操作都可以在数字末位加一个或使得对方下一步不可能赢. 比如现在数字是, 加了或之后变成或, 这样的话平方数不可能以或结尾, 那么对方下一回合不在末尾加数字就赢不了. 于是对方就只能把数字变成或者, 但三位以上的平方数的话相差都不小于, 那么连着从到这个数字劈两半总有一半一个平方数都没有, 所以选好一点对方就没法赢. 这么一想这个初始数字也就只能保证没法开局赢, 剩下就是无限加数的内卷 (摊手).

　　A初P5. 红大, 就是难得算一点点...... 反正这种题我应该会直接列方程算...

　　A初P6. 其实是一个脑筋急转弯题, 考虑, 结果用整数的条件就有, 全部加起来就完了.

　　A初P7. 挺套路的题目. 反正先编号, 甲每次可以拿奇数号的也可以拿偶数号的, 但是甲拿完后乙就只能拿和甲相反的奇偶性号码的面包. 然后不妨假设奇数号的果酱的至少十个, 然后先从奇数号开始拿, 考虑参数拿到的果酱面包数量+剩余的编号为偶数的果酱面包数量, 如果这个参数不超过的话就拿奇数的, 超过了的话就拿偶数的, 这样就行了. 不过这个题, 英文版的题目是果酱面包和蜂蜜面包, 俄文答案里面写的是加糖和加肉桂??? 这? 英语国家的人没有cinnamon和sugar吗?

　　A高P1. 拿. 就也不是看不上这题, 但是这个画风真的感觉像是小学时候会在课外书上看到的那种智障一样的智力测试题...

　　A高P2. 固定一条对角线, 欧拉路的起点和终点在棋盘染色下不同色, 所以一条对角线上不可能同时有终点又有起点. 于是车的所有步数中至少步会涉及对角线, 即要么从对角线出来, 要么走回对角线. 但是对角线旁边的两条次对角线只有个格子, 所以一定存在一个格子满足条件.

　　A高P3. 答案是. 实际上不妨设甲初始位置为, 依次跳过位置向量为的朋友的话最终落地点的坐标为. 这样的话实际上落地点个数等价于一半朋友加负号一半朋友加正号的选法.

　　A高P4. . 就, 硬分析讨论的题, 还挺烦的.

　　A高P5. 几何我就不评论了. 不过这题是个导角题, 就, 导一导就好了.

　　A高P7. a) 不一定, 意思是下图中间那个红四边形的两组对边分别各自两头延长, 一头相交, 另一头拉老远了截一下变成三角形, 于是就可以两个三角形覆盖表格, 但是任何一个格子都不是由一个三角形就盖住了的. b) 一定, 但是答案分类讨论了一页, 我懒得看了, 这种题做起来也烦人. 要考CMO的同学可以考虑拿这个题练习一下写东西, 毕竟, 说真的也不难, 但就是不好写, 跟去年那个P2一样, 所有人都算得出正确结果, 但是一堆3分6分的...

　　就这样吧, 明天应该会发Metropolises的题, 只要官网放出来的话. 不过说起这个Metropolises, 之前在哪看到管这个叫大都会, 但是大都会这个题就一直给人一种大资产阶级纸醉金迷的夜上海既视感? 行吧, 也不知道今年中国派哪个省去的.

　　另, 老龙前两天发了伊朗几何的题 (I, A), 大家去看看呀~

　　作者

　　偽同文算學 乙一

本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢