用消点法解2020年CMO第4题
一年一度的中国数学奥林匹克(即数学冬令营,简称CMO)于11月22日至28日在湖南长沙长郡中学举行。来自全国的近500名数学高手逐鹿中原,大显身手。
昨天和今天早上8:00-12:30进行考试,每天三个题目。6个题目中今天的第4题为几何题。题目如下:
WINTER
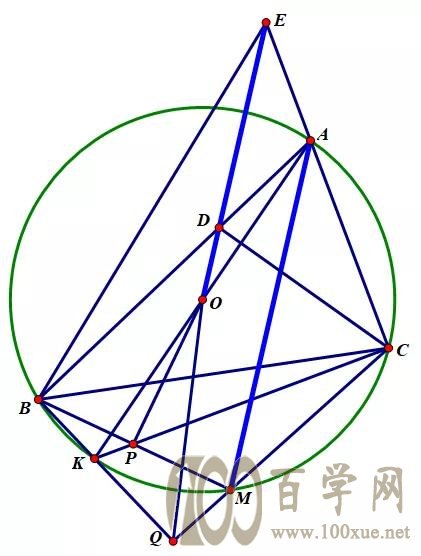
锐角△ABC中,AB>AC,M为其外接圆上劣弧BC中点,K为A的对径点。过O作OD//AM交AB于D,交CA的延长线于E。直线BM交直线CK于P。直线CM交BK于Q。
求证:∠OPB+∠OEB=∠OQC+∠ODC
第一步,根据题意画出准确图形。
本题条件比较普通,没有特别的限制,
按条件准确画图就行,没什么难度。
但是要注意图形中EOQ不共线。
第二步:老规矩,先从条件入手,看看图
形中有哪些隐藏的性质。
由M为弧BC中点知AM为∠BAC角平分线,
由OD//AM知∠AED=∠ADE,
由直径知∠ABK=∠ACK=∠AMK=90°,
当然还有OM⊥BC.
其他的似乎就是圆周角相等之类的性质了,
暂时没有发现很好的结论了。
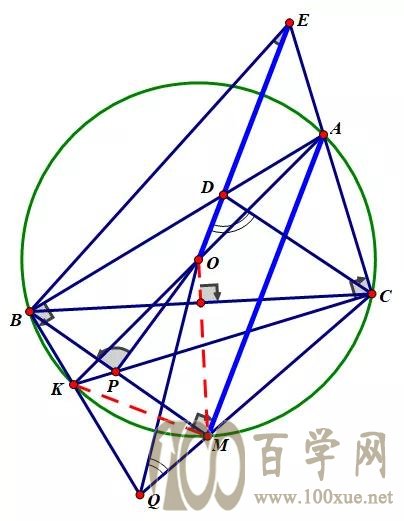
第三步:从证明结果入手。
这个结果还是比较奇怪的,
要证明两个角的和等于另两个角的和,
一定要把角度看清楚,
稍微看走眼就会南辕北辙、误入歧途。
zui.好把这四个角都标记出来,
要证∠OPB+∠OEB=∠OQC+∠ODC
基本思路就是倒角,把这两组角都倒
到某个三角形或者其他图形中。
但是四个角似乎都不好倒出去,
没法直接传递到其他的角。
如果根据四边形内角和,把求证结论等价转化为
∠PBA+∠POE=∠DOQ+∠DCQ,
还是没法传递出去,似乎意义不大。
到这里就陷入了迷茫,分析法好像走不下去了。
第四步,下面只能结合求证,进一步挖掘已知图形的性质了。
直接证明不行,估计要适当添加一些辅助线,
已知中最重要的线显然是直线EO,可以考虑做出整个
直线,这样它与图形下半部分其他线也会相交。
还是希望倒角,我们先关注其中的一个,例如∠OPB,
最常用的倒角技巧当然是通过共圆,
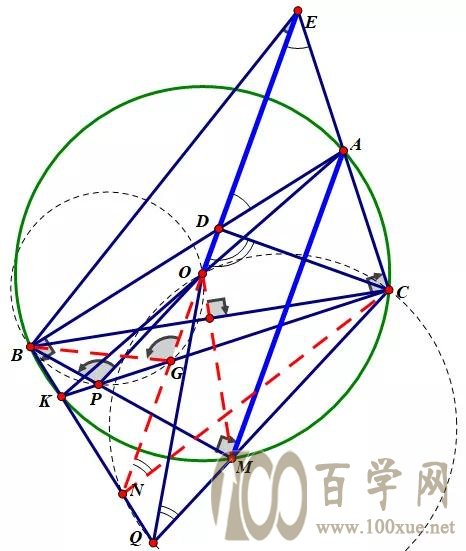
在准确的图形下面,似乎OBPG共圆,其中G为
OE和CK交点。这个倒角不难证明。
这应该是一个重要的结论,因为这样就能把∠OPB和∠OEB
转移到△EBG中,看到了希望!
对称的QNOC共圆,其中N为OE,QB交点。
这样本题就转化为求证∠EBG=∠DCN。
第五步,至此把证明简化了,应该在正确的道路上越走越远了。
然而乱花渐欲迷人眼,
图形太乱了,到了这里就能考虑消点,
就能把无关的P,Q,M及与他们相关的元素消去。
得到下图,
条件变为:已知AK为直径,过O的直线满足AD=AE,
求证:∠EBG=∠DCN。
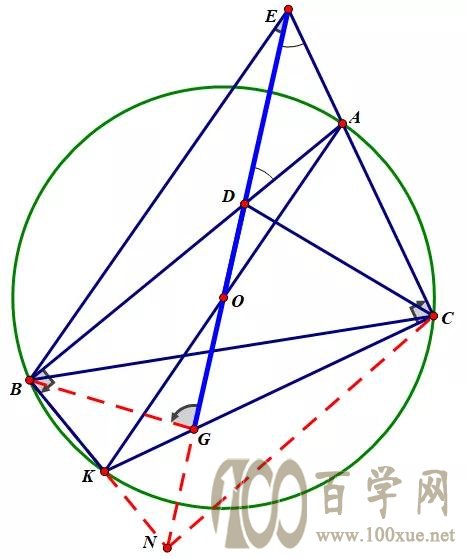
要证明此两角相等,基本思路是倒角或相似,
但是似乎也都不太容易。
只能进一步挖掘图形性质,
容易发现△BDN∼△CEG,
结合准确的图形,可以大胆猜测,
图形中还有很多等角,
即∠DBG=∠DCG,∠EBN=∠ECN。
由对称性,只需证明第一个,
第六步:
这样就能进一步消去点E,N及相关元素,
简化图形,得到下图:
已知AK为直径,求证∠DBG=∠DCG,
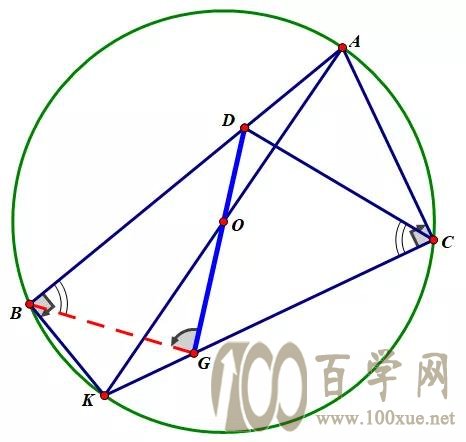
因为没有其他条件了,证明的基本思路当然还是倒角,
考虑到圆周角,所以自然的思路是延长BG,CD交圆于I,J,
下面只需证明IOJ共线即可,而这显然是帕斯卡定理。
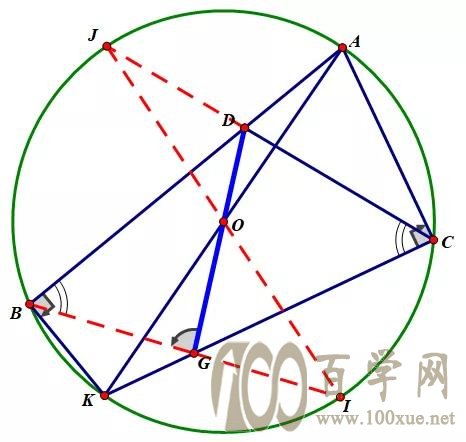
这样就能对称的得到另一对等角,从而水落石出,本题得证。
第七步:
最后将证明过程整理好,书写如下:
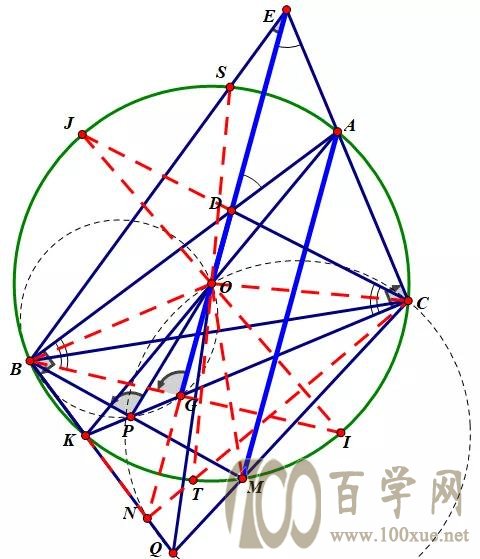
证明:设DO交CK,BK于G,N。CD,CN,BG,BE交圆于J,T,I,S,
由AK为直径知∠ACK=90°,
由M为弧BC中点知AM为∠BAC角平分线,
结合OD//AM知
∠EGC=90°-∠AED=90°-∠CAM
=90°-∠BAM=∠OBP,
故OBPG共圆。
对称的ONQC共圆。
对圆内接六边形CKABIJ利用pascal定理知IJO共线。
故弧JK=弧IA,故∠DBG=∠DCG。故∠KBG=∠ACD。
对称的,对CAKBST由pascal定理有SOT共线,
故∠EBN=∠ECN。
则∠EBG=∠DCQ。
故∠OGB+∠OEB=∠ONC+∠ODC
即∠OPB+∠OEB=∠OQC+∠ODC。
第八步:简单总结。
综合上面的思考过程,可以看出本题是一个难得的好题。
难度合适,题目新颖,既朴素自然,中规中矩,结果又出人意料,不落窠臼。
证明不太容易入手,四个角度都不好处理转化,然而找到了入手点后,不需要太多过程。
当然本题思路比较多,应该还有更简洁明了的证明方法。
本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用,绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系(底部邮箱),我们将及时更正、删除,谢谢

