再说高考压轴题应不应该用成题

　　您认为高考压轴应不应该用成题?

　　2021年高考今天落下帷幕，各省试卷使用情况如网图所示：

　　全国甲卷：云南、广西、贵州、四川、西藏

　　全国乙卷：河南、山西、江西、安徽、甘肃、青海、内蒙古、黑龙江、吉林、宁夏、新疆、陕西

　　新高考一卷：山东、广东、福建、江苏、湖南、湖北、河北

　　新高考二卷：海南、重庆、辽宁、

　　地方自主命题省市：北京、天津、上海、浙江

　　迄今，已经出现了三份完整的试卷，分别为全国甲卷、乙卷和新高考一卷。现在看来，压轴题依然是成题。去年高考刚结束我就写文章说过此话题(高考压轴题应该不应该用成题?)，阅读量为1.6万，说明大家的关注度还是很高的，并做了个投票，有2644人参与了投票，结果如下:

　　从结果看仅有5%的人赞成用成题，11%的人无所谓，82%的人觉得不应该。今年投票继续，看大家有没有改变立场。

　　先说清楚两个概念：

　　压轴题：是指高考题中最难的两个题，一般是最后两个解答题(如果最后一题是选修题，则不算压轴题)，通常是解析几何和导数，有时候也可能是概率统计或者立体几何等。

　　成题：一般指现成的题目，即已经在杂志书籍资料或者考试中出现过的题。可能是很经典的有上百年的结构或者模型。

　　这三年高考数学全国卷压轴题成题很多，而这两年尤甚，几乎所有的压轴题都是成题，都能在常见的资料中找到出处。

　　先看全国甲卷的第20题:

　　此题结构优美、结论简洁。但是是非常老的结构，一般称为彭色列定理，相关的恒等式称为欧拉察柏公式，本公众号三年前的文章(《圆锥曲线中的欧拉察柏公式相关问题》)基本把相关问题总结完了，此文也收入了拙作《鸡爪定理》[1]的附录中。在此再温习一下：

　　此结构对两圆、及两圆锥曲线都成立，甚至可以推广到空间中。国内最早见到的是1982年高考压轴题：

　　此题就是两个抛物线的情形，证明完全类似，一般都是用韦达定理解决。

　　在前面的文章(《抛物线6——圆锥曲线讲义之十七》)中，我又提到了这个题目和韦达定理的解法。

　　此题还作为2011年高中数学联赛B卷一试的压轴题考察过。

　　此类问题还作为2009年清华大学保送生考试试题，不难发现上述高考题和此保送生考试题几无二致。

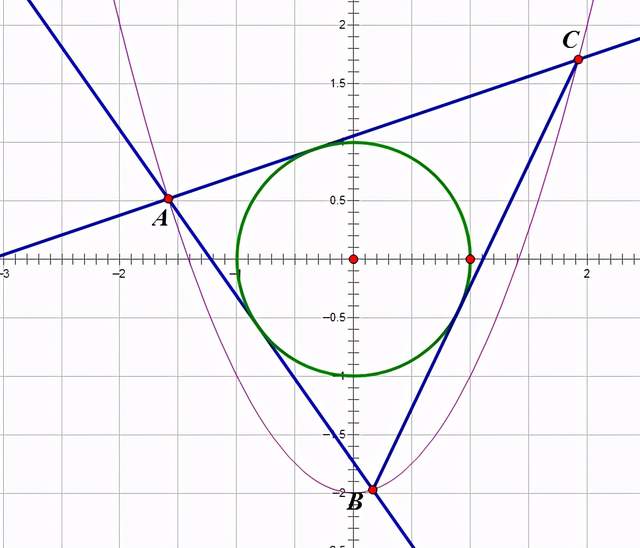
　　此题还作为2014年浙江的高考题考察过。

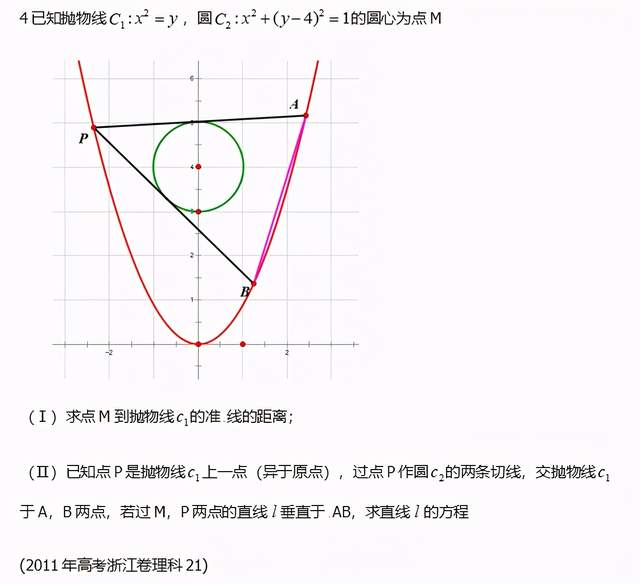
　　此结构人见人爱，作为高考、自主招生或者联赛都很适合，2017协作体也作为联赛模拟题考察过。

　　当然此结构还作为2009年江西高考文科的压轴题考察过。

　　上述题目的证明思路基本都是如出一辙的利用韦达定理解决即可。具体解答过程可以参考上述我公众号的文章。

　　下面看全国乙卷的最后一个压轴题，

　　此结构也是很经典的，一般称为阿基米德三角形，相关的文章汗牛充栋。我在圆锥曲线系列中研究过很多此三角形的性质，在文章(抛物线2——圆锥曲线讲义之十三)中的问题8为:

　　8、动直线l过P与C交于A、B;过AB的切线交于M，(1)求M的轨迹方程

　　(2)求△MAB面积的最小值;

　　不难发现上述两题异曲同工，基本思路都是设出切点坐标，求出交点及三角形面积表达式，到此都是完全相同的。然后将交点带入限制条件中(我那题点在直线上运动，本题中点在圆上运动)，利用函数或均值不等式求出最值即可。

　　最后看新高考全国1卷的最后一个压轴题：

　　这还是一个老生常谈的问题，比较早的资料中都有，例如1983年出版的《数学题解辞典(平面解析几何)》[2]中多次提到此结论，最后在一般的圆锥曲线中将其证明并系统的介绍其退化的情形如下：

　　其证明思路基本上要么用曲线系秒杀，要么用参数方程巧算，当然直接联立蛮算亦可。

　　我在《圆锥曲线系列讲义之九》也讲到了此两种情形，并提示用参数方程计算比较方便。

　　当然此结论在全国卷的高考题中也是屡见不鲜，例如

　　其退化的情形也是高考中的常见问题，例如：

　　2011年全国高中数学联赛一试的最后一题为此题逆命题;

　　由以上不难发现此三个问题都是非常古老的问题，作为平时测试和练习非常合适。但是作为高考真题并不合适，因为这很不公平。对于熟悉此结构的学生基本就是默写答案，而没见过此结构的学生绞尽脑汁也无法在短时间内解决。

　　您觉得呢?

　　参考文献

　　1 鸡爪定理 金磊 2020年6月 哈尔滨工业大学出版社

　　2 数学题解辞典(平面解析几何) 唐秀颖 1983年 上海 辞书出版社

本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用，绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系(底部邮箱)，我们将及时更正、删除，谢谢