自主招生数学竞赛如何准备,如何拿到奖!
在自主招生中,五大学科竞赛绝对称得上是硬通货了。那参加2018年高考的竞赛生表现又是怎样的呢?以清北为例:
奖项北京大学清华大学
|
奖项 |
北京大学 |
清华大学 |
|
国一 |
107 |
63 |
|
国二 |
162 |
143 |
|
国三 |
67 |
53 |
|
省一 |
166 |
203 |
|
省二/省三/无奖项 |
322 |
449 |
|
总计 |
824 |
911
|
从上表可以得到结论:获北大降分的824人中具有省一及以上奖项的共502人,占比为60.92%;获清华降分的911人中具有省一及以上奖项的共462人,占比为50.71%。清北两校合计获自招降分的考生有55.56%,竞赛生占据了清北自招的大半江山。
由此可见竞赛在自招过程中的重要程度,而数学联赛可以说是五大学科竞赛中最难、历史最久、竞争最激烈的一项赛事了。要想在数学竞赛种拿奖,冲刺国奖、省一确实不容易,但拿个省二省三,几率还是相当大的。
数学联赛小科普
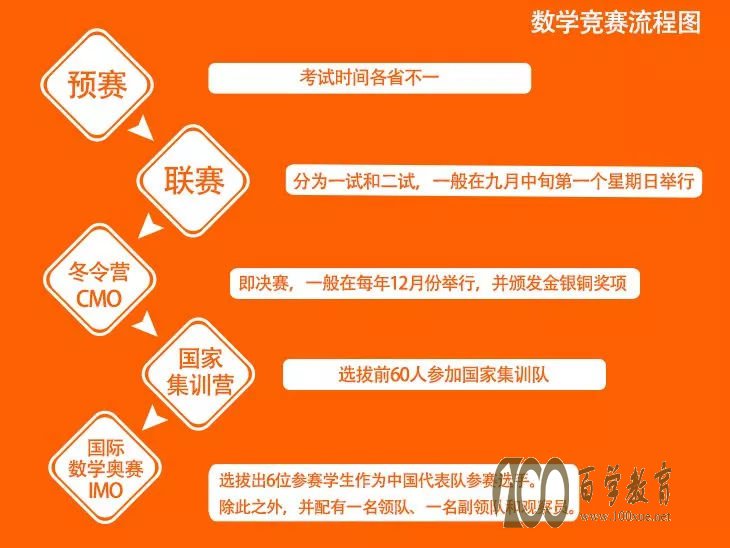
全国高中数学联赛预赛由各省市自治区根据省情决定是否举办,由各省市自行命题划线,一般省份均有预赛,但像北京就不存在预赛,可以直接报名参加全国高中数学联赛(即通俗说的复赛)。 全国高中数学联赛复赛分为一试和二试:一试考试时间80分钟满分120分,二试考试时间150分钟满分180分,一试二试得分总和为复赛总分,而这一阶段也将诞生省一、省二、省三。
其中省一是由中国数学会对其试卷审核后确定获奖的,每年限定一等奖名额1000名左右,并划分到各省、市、自治区。
冬令营(CMO):在全国高中数学联赛中取得优异成绩的学生有资格参加由中国数学会奥林匹克委员会主办的“中国数学奥林匹克(CMO)暨全国中学生数学冬令营”(决赛),并颁发金银铜奖项(即国一国二国三),每年约200人,分配原则是每省市区至少一人,然后设立分数线择优选取。
国家集训营:冬令营中排名前60的选手组成参加当年国际数学奥林匹克的中国国家集训队,国家集训队成员均为金牌。
国际数学奥赛(IMO):经过集训队的选拔,选出6位参赛学生作为中国代表队参赛选手。除此之外,并配有一名领队、一名副领队和观察员,最终参加国际数学奥林匹克(IMO)。
从高中数学联赛到国际数学奥赛,一个竞赛生的竞赛之路就结束了,而每一位参加竞赛的同学能达到的阶段不同,那么不同阶段对未来升学又有怎样的帮助呢?
|
竞赛成绩 |
优惠政策 |
|
进入国家队 |
保送清北 |
|
进入国家集训队 |
保送清北 |
|
全国决赛金牌 |
签约清北 |
|
全国决赛银、铜牌 |
获清北自主招生资格 |
|
强省省队 |
签约清北 |
|
省一等奖 |
参加清北金秋营、交大致远营等竞赛营取得签约 |
|
省一等奖 |
获交大、浙大、中科大自主招生资格 |
|
省一、省二等奖 |
获南大、同济、北理、北邮等自主招生资格 |
|
省三等奖 |
其他高校自主招生资格 |
竞赛生涯规划
既然竞赛获奖好处颇多,那么对于学生和家长来说,如何合理规划竞赛学习最终拿到奖项就显得尤为重要了!
私享课竞赛体系
对于在初中阶段已经进行竞赛学习,并有一定基础的同学,在整个高中学习的不同阶段,我们又该如何规划呢?下面奉上干货!
高一阶段
新高一暑假到高一上学期 初升高是竞赛生第一次真正意义上开始高中竞赛学习,建议充分利用好暑假,完成高联一试和平面几何的学习。
高联一试的知识点与高考基本一致,所有知识在初三一年应该已经基本掌握,现在要做的就是提高技巧和熟练度;而平面几何在高联二试的四道大题(几何、代数、数论、组合)中一般比较容易,而且初中已经有了基础,平面几何的学习应该是比较轻松的。
一试推荐书籍
《奥数教程》由华东师范大学出版社出版,高一、高二只有基础篇,这一系列共分三本,分别在封面注明了高一到高三三个年级。
《高中数学竞赛培优教程(一试)》(李胜宏),内容非常系统和全面,题目难度适中。
平面几何推荐书籍
《奥赛经典——奥林匹克数学中的几何问题》,主要由沈文选老师编写,湖南师范大学出版社出版。重点在第一篇,除了三四五六七章(从托勒密到九点圆)可以略看,不是考察重点,其他都要认真看。
建议可以拓展的内容
l 集合的基数与分划。
l 函数极值问题的方法拓展。
l 函数凹凸性。
l 高等数学初步。
l 数列进阶知识(高阶等差数列,不动点法等)。
l 三角恒等变形。
l 向量法在立体几何和解析几何中的应用。
l 函数迭代与抽象函数。
l 不等式的证明技巧拓展。
l 利用参数方程解几何问题。
l 解题方法拓展(包括归纳法,反证法,构造法和极端原理等)。
l 计数问题的拓展(递推,容斥原理等)。
l 多项式的差值与差分。
l 母函数方法。
高一寒假到高一下学期 这一阶段算是高中竞赛学习的第三个阶段,这一阶段要开始接触二试部分较难知识(数论、组合)。二试还有三块重要的内容你需要接触:代数、数论和组合。
关于代数部分的学习
l 高斯函数。
l 周期函数,带绝对值的函数。
l 进阶三角函数(三倍角公式,三角不等式等)。
l 数学归纳法进阶(第二数学归纳法,广义归纳法)。
l 进阶的函数递归,特征方程法。
l 函数迭代,函数方程。
l 平均不等式进阶。
l 进阶不等式:柯西不等式,排序不等式,琴生不等式等。
l 不等式解题策略。
l 复数进阶(指数形式,欧拉公式,单位根等)
l 组合恒等式。
l n次方程(多项式)。
代数不一定考,要考也只能是不等式或者数列函数等和一试紧密联系的部分。
推荐书籍
《数学奥林匹克小丛书》中代数内容,属于进阶的数论书,适合在入门后阅读。
高二年级的《奥数教程》提高篇不等式的部分,难度适中可作为入门书籍。
关于数论部分的学习
初等数论知识与高考内容联系不算紧密,需要额外的学习。可以说初等数论有大量的小定理和小结论,并有很多解题方法需要掌握。
参考联赛大纲,需要学习的知识基本包括整除,素数,同余等基本知识,并且需要自己形成对于数论问题的一套处理思路,并需要熟练运用一些常见的数论定理。
参考联赛大纲,需要学习的知识主要总结如下:
l 数的整除,质数。
l 公约数,公倍数,分解质因数,剩余类等。
l 同余问题,丢番图方程。
l 数论基本方法:无穷递降法,欧几里得辗转相除法等。
l 重要数论定理:费马小定理,欧拉函数,孙子定理和裴蜀定理等。
推荐书籍
《数学竞赛研究教程》中的数论部分。
《初等数论》,为大学教材,可以适当参考。
关于组合部分的学习
组合数学与高考内容的计数原理,排列组合在知识上一脉相承,但问题类型上差距较大,想要入门竞赛组合题,还是需要练习和竞赛教师的指导。
可以说组合问题有一定的能掌握的共性和手法,但仍然很大程度上依赖天赋和运气,知识并不算太多。
参考联赛大纲,需要学习的内容除了要熟练的掌握高考中的计数原理,排列组合外,还需要学习图论等知识,并掌握组合极值问题的常用方法。
参考联赛大纲,需要学习的知识主要总结如下:
l 基本计数原理:加法原理,乘法原理。
l 排列问题,圆周排列等。
l 组合问题。
l 计数问题的常见模型:走格问题,排队问题,染色问题等。
l 一些常用定理:抽屉原理,容斤原理,极端原理等。
l 组合问题常用方法:算两次,调整法,构造法,递推法,母函数法等。
l 组合极值问题。
推荐书籍
《奥数教程》的计数原理内容。
《数学奥林匹克小丛书》11、13册,由张垚老师编著,难度梯度设置合理,知识覆盖全面,题目典型而有深度,解答细致易懂,可以作为一本十分优质的入门书籍。
《数学竞赛研究教程》中的组合部分也应当参考。
高二阶段
新高二暑假到高二参赛 这个阶段就是验收成果的时候了,你直面的就是数学联赛。多做历年真题,积累考试经验。
这一阶段,不再过多推荐新的书,我们把侧重点放在复习之前学习的书籍上。但是有一本刊物:《中等数学》,它每年到了暑假就会发行几本增刊,有一本收集了上一年全国乃至全世界各地的考题,有一本就是各省的竞赛名师专门为联赛命制的模拟题,后者是你准备联赛的利器。
考前推荐书籍
《数学奥林匹克小丛书》
《奥数教程》
《数学竞赛研究教程》
《高中数学竞赛培优教程》
二试推荐书籍
《高中数学竞赛培优教程》作为复习知识来用。
《数学奥林匹克命题人讲座》、《走向IMO》可以作为进阶练习。
高二联赛后到高三联赛 高二的联赛是很重要的一个分水岭。如果你的目标是强省的省队,国赛金牌,集训队甚至更远,下面的推荐适合你。如果你的目标没有这么远,剩下的内容你可以完全忽略,前几个阶段的事情,你大可放慢速度。
代数推荐书籍
《奥数教程》中的高三年级多项式部分建议刷完。
《数学奥林匹克小丛书高中卷5不等式的解题方法和技巧》,由苏勇和熊斌两位老师合著。
数论推荐书籍
《数学奥林匹克命题人讲座——初等数论》由冯志刚编写,上海科技教育出版社出版。题目质量着实很高,一道道刷过来,数论的能力会有质的飞越。
组合推荐书籍
《奥赛经典——奥林匹克数学中的组合问题》,这是组合这一块综合性的大百科全书,除了第一二章可以略看,后五章要认真刷完,对于组合能力的提升要很大的帮助。
《数学奥林匹克小丛书高中卷13组合极值》、《高中数学竞赛专题讲座——组合构造》都是由冯越峰老师编著,二选一即可。
高三阶段
新高三暑假到高三联赛 这一阶段,是学生在一系列拔高练习之后的回归期。在这一阶段,需要做好两件事。首先,把之前刷过的所有书都要过一遍,作为复习。
其次,高二暑假出来的那一本《中等数学》的增刊需要完成。复习过程中,多参见前面的推荐书目
从高三联赛到CMO 如果学生考进了省代表队,并且有资格参加国赛,那么数学竞赛之路还能继续往前走。联赛结束到国赛开始,还有一段时间,在这个阶段,学生需要刷的是三本书。
推荐书籍
《数学竞赛研究教程》的上下册
《奥数教程学习手册》高三年级
《走向IMO》系列丛书
本站(www.100xue.net)部分图文转自网络,刊登本文仅为传播信息之用,绝不代表赞同其观点或担保其真实性。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系(底部邮箱),我们将及时更正、删除,谢谢





